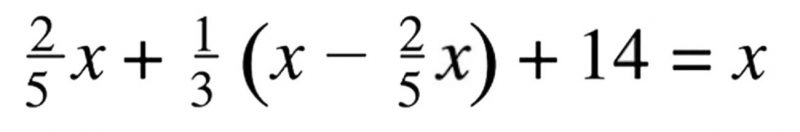Coleman: To Solve the Problem Below, Try Using a Tape Diagram. It’s an Example of How Different Ways of Doing Math Can Make Hard Problems Easy
Major news outlets spend little time covering mathematics, so imagine my surprise — and pleasure — to see that one of the most popular pieces this summer in The New York Times addressed, of all topics, “the order of operations.” The story concluded, “Let’s spend more time teaching our students the more beautiful, interesting and uplifting parts of mathematics. Our marvelous subject deserves better.”
As an educator who has spent the past 16 years teaching mathematics, I couldn’t agree more. And that made me think: What might be another common challenge facing teachers, and why not explore it with readers?
So here goes.
In my classroom, I frequently encounter parents inquiring about the push to learn more conceptual math than when they were growing up and why students need multiple strategies for solving problems. Some suggest that simply learning the standard algorithm for a math problem (2+2=4, 6×8=48, etc.) is enough. Some, who really didn’t like math, might even say it’s more than enough.
I agree that students need to learn the set of rules or procedures that can be followed when doing calculations. In some cases, that’s the best tool for the job.
But in most instances, students need options — more tools in their toolbox. There might be better ways of solving the problem, and by knowing multiple strategies, students understand which operation or algorithm to use in a given situation. They also gain a deeper grasp of mathematics and how to apply it in daily life.
Still with me? OK, consider the following problem.
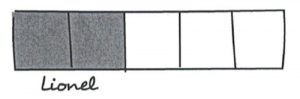
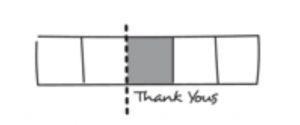
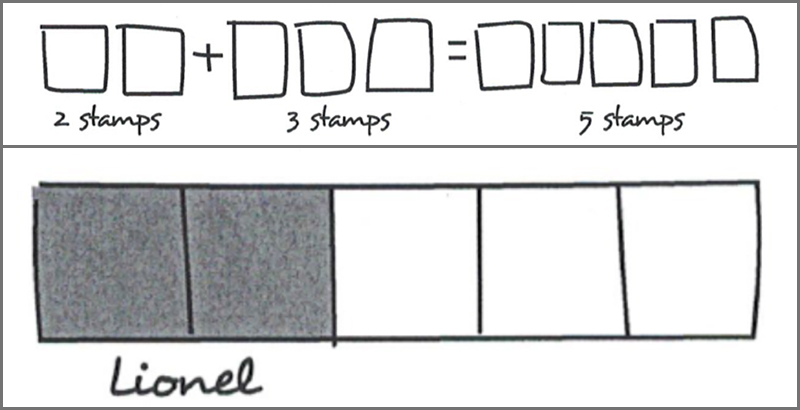
Zoe had some stamps. She gave 2/5 to Lionel. She used 1/3 of the remainder to mail thank-you notes. She had 14 stamps left. How many stamps did she have when she started?
This is a very tough problem to solve if you know only the algebraic approach or standard algorithm. Which numbers go on the left side of the equation? Which ones go on the right? What are the missing variables? What is the order of operations?
But with the use of tape diagrams, a mathematical model used today that helps students visualize numbers, a fifth-grader can solve the problem in under a minute. Here’s how.
In kindergarten, students learn to divide numbers into units using a conceptual approach, starting with concrete examples such as apples or blocks — or stamps.
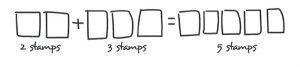
In third grade, they learn the concept of fractions, such as two stamps out of five stamps is equal to 2/5 of the whole number of stamps.
By fifth grade, students can use this method to easily solve the stamp problem above in four steps.
1. Because Zoe gave two-fifths of her stamps to Lionel, we know this can be divided into five units, and that Lionel got two of those. Three units remain.
2. We know that one-third of the remainder — one of the three units — was used to mail thank you notes.
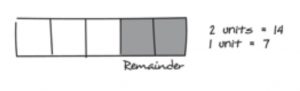
3. We know that the remaining two units equal 14, and that they’re the same size. 14 divided by 2 equals seven stamps in each unit.
4. Now it is easy to multiply seven stamps by five units to get the answer: 35 stamps.
Yes, we could have set up the problem this way:
But how much harder is it for students to remember this? For adults, forget about it.
We’re limiting our students if we give them only one set of tools for solving math problems. In school districts around the country that are increasingly using conceptual approaches to teach math, there is more evidence every day that students are thriving.
They’re loving math. What’s more they, and we, are talking about math. I call that a win.
LauraMarie Coleman works with and coaches teachers on professional development for Great Minds. Previously, she was a special education classroom teacher and an instructional coach, working with alternative and special education students and teachers in grades K-8, in Binghamton, New York.
Get stories like these delivered straight to your inbox. Sign up for The 74 Newsletter

;)